1 號分支：變化短手數
不論駒余與否都可以接受，因為玉將方已經沒有採取最善防禦了。
變化與紛れ
本篇將介紹「變化」與「紛れ」的含義以及相關的延伸內容。由於內容將涉及大量的手順分支圖，以下先說明各符號所代表的分支屬性。我們會在分支的結尾使用不同符號來表示該手順是否有詰，以及是否存在駒余：
| 沒有駒余 | 駒余 | 有無駒余皆同 | |
|---|---|---|---|
| 有詰 |  |  |  |
| 不詰 |  |  |  |
我們的立場
在詰將棋中，因為題目的棋駒配置，有時候容易產生一些容易誤導的設計，這些問題可以分為兩類：瑕疵與缺陷。
-
瑕疵
相比缺陷較為輕微。常見的例子為：變同、變長。出現這類問題時，通常歸因於創作者未盡完善，但對解題者而言，並不會造成實質「損害」。
-
缺陷
缺陷，或稱為重大缺陷，會影響解題本身，例如：不詰、余詰。其中「不詰」指題目本身無解，這已非解題者能力問題，而是題目設計失當。
實務上，帶有瑕疵的題目仍可以被當作一般作品，出現在詰將棋平台或書籍中。不過在我們的進階篇中，我們會以較嚴格的標準看待瑕疵。因此，在後續教學中，雖然某些問題屬於可採用的瑕疵類，但基於說明便利，皆一律視為不採用處理。（讀者仍要具有自行判斷的能力）
本詰
本詰可以理解為「正解手順」。每題設計好的詰將棋必定包含一個正解手順。在綿貫規約中，本詰必須唯一，並且不能駒余。而現今主流規範在此基礎上進一步拓展，納入了部分
準詰相較於本詰，準詰可能是駒余或是最終手余詰等的其餘分支。
一同存在的題目。
以下，我們將以一個現今可被採用的「五手詰」作為例子進行介紹。在五手詰中，本詰只能長這樣：
五手詰的本詰
前面提到，本詰不能有駒余的情況存在。如果初始配置中有無用持駒或解題過程中獲得的棋駒未使用完畢，將導致該題判定為不完全作，無法被採用。
本詰不能駒余
変化
當玉將方發生分歧時，稱之為「變化」。變化本身並不含有「詰」的涵義，變化可以有詰，也可以沒有詰。
一題完美的詰將棋，必須讓所有的變化都有詰，只要有一個變化沒有詰，本題詰將棋將被視為不詰 。不詰屬於重大缺陷，會使該題直接變不完全作。當詰將棋的變化越多，其評價也會越高。
有詰的變化可以依據手順長短與是否駒余，繼續區分為以下幾種：
變化短手數
先來看比較簡單的種類，比本詰還要短的變化，稱為「變化短手數」。
變化短手數是由於玉將方沒有採取最正確的防禦手段，而導致提早有詰。這類變化不論駒余與否皆無傷大雅，不會影響本詰的地位。
變化短手數有無駒余都沒問題
變化同手數
當變化的手數繼續增長，達到與本詰相同手數時，稱為「變化同手數」。
變化同手數因為與本詰手數相同，可能會威脅到本詰的唯一性。看看手順圖中的兩種變化同手數：
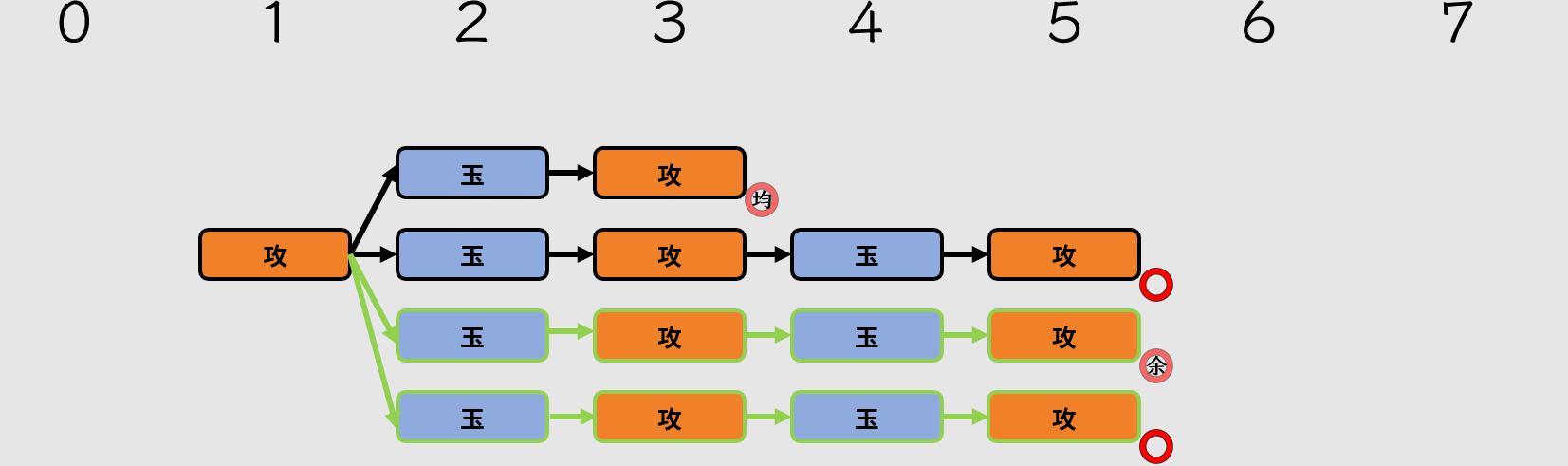新增了綠色分支
探討一下沒有駒余的變化同手數分支吧。在第二手玉將方產生分歧後，居然也可以做到五手詰，並且沒有駒余，直接挑戰了本詰的唯一性。如果遇到這種題目，在回答或書寫正解手順時，可能會不知道該選哪一個。雖然兩者都屬於正解，但似乎存在「兩個」正解，令人不快。
遇到這種情況，代表存在瑕疵，會使該題不採用。
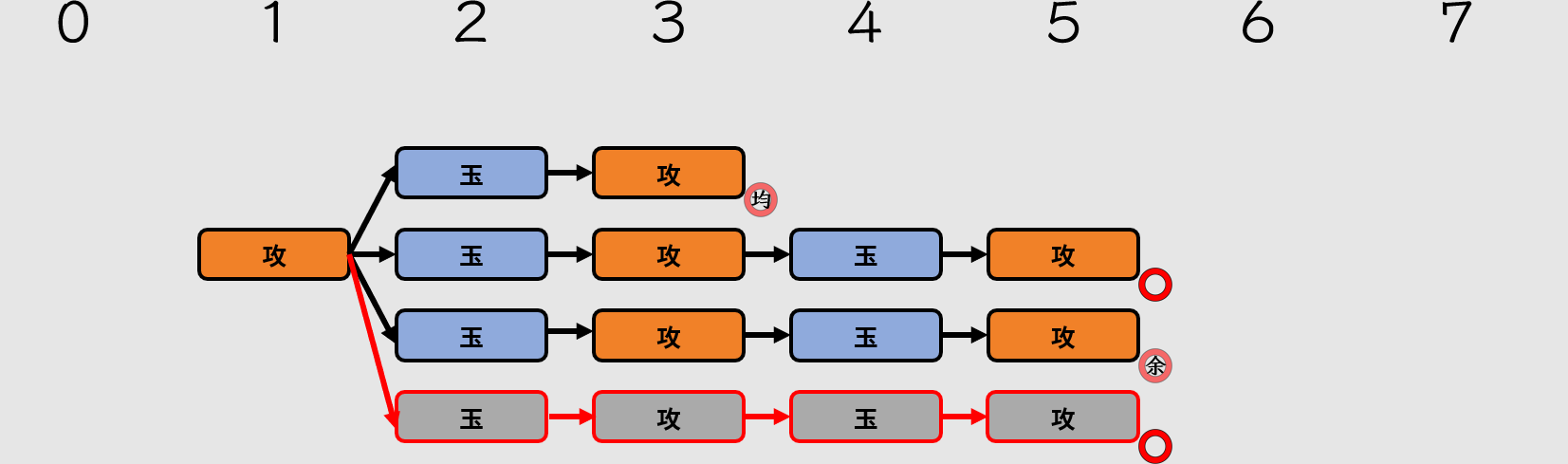變化同手數不駒余，不能存在！
不過，變化同手數除了在最初發生分歧，還可以在第四手發生分歧。例如：
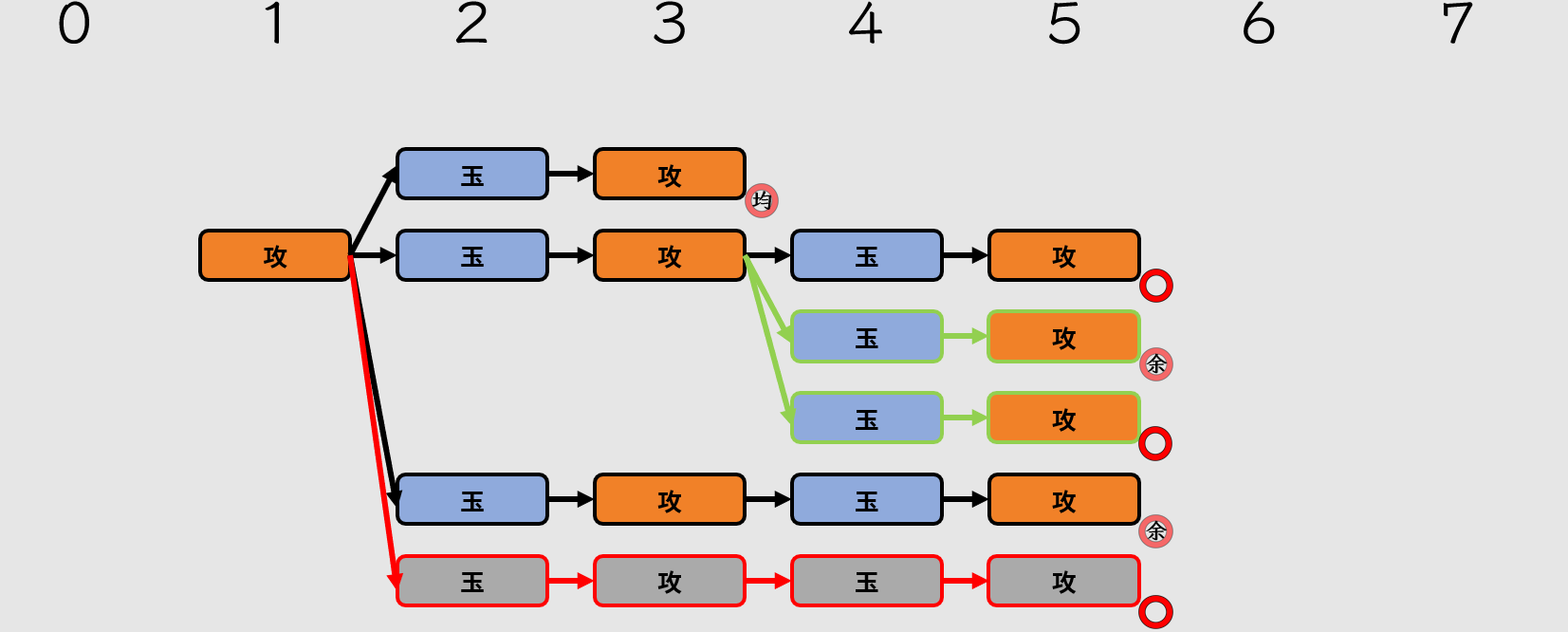新增了綠色分支
雖然前面提到，與本詰手數相同且不駒余的變化，因為與本詰屬性一致，會導致該題喪失唯一性，所以不能出現。但是但是，如果變化同手數不駒余發生在最終二手，也就是最後一次玉將應手的分歧（這裡為第四手），則屬於「最終二手變同」，此類情況又可以被接受。
最終二手變同，可以存在
變同
在許多詰將棋網站或書籍介紹規則時，經常會以「變同是一種瑕疵」簡短帶過，導致許多人誤以為「變同」是「變化同手數」的縮寫。
其實不然，「變同」實際上是「變化同手數不駒余」的縮寫。 也因為如此，才會強調變同屬於瑕疵，但最終二手變同可以接受。
變化長手數
當初第一次看到「變化長手數」，差點顛覆了我對「幾手詰」的概念，心臟漏了幾拍。因為「變化」等於「玉將方發生分歧」，如果有某個變化可以比本詰更長，那為什麼它仍然屬於變化呢？照理說，它不是應該會變成本詰，而原本的本詰則變成變化短手數嗎？
請再度回想一下綿貫規約。綿貫規約中，有以下兩條規定：
- 玉將方須選擇最長手順〈應手最長律〉
- 本詰不能駒余
然而，這兩條規定有可能出現互相矛盾的情況。我們來看一個範例：
範例
（出自CrossingVoid）
大家覺得哪一個應該被視為本詰呢？如果玉將方選擇了最長手順，就會產生駒余；選擇不駒余，手數卻會變短。雖然已經看到了「變化長手數」的標題，結果已無懸念。沒錯，在這種情況下，長手數的反而是變化，不駒余的才是本詰。
針對這種情況，我們可以對綿貫規約的第七條（玉將方須選擇最長手順〈應手最長律〉），進行擴增解釋為：「玉將方在不駒余的情況下須選擇最長手順」。也就是說，不駒余的規則優先於最長手數，凌駕其上。
不過需要注意的是，「變化長手數駒余」最多只接受延長二手——即「二手變長」，超過四手以上的，會被判定成缺陷。而且現今的題目怕有爭議，出現這種題目已經實屬罕見，通常不會採用，或是至少會標註「有變長」。
來看看新的變化長手數分支：
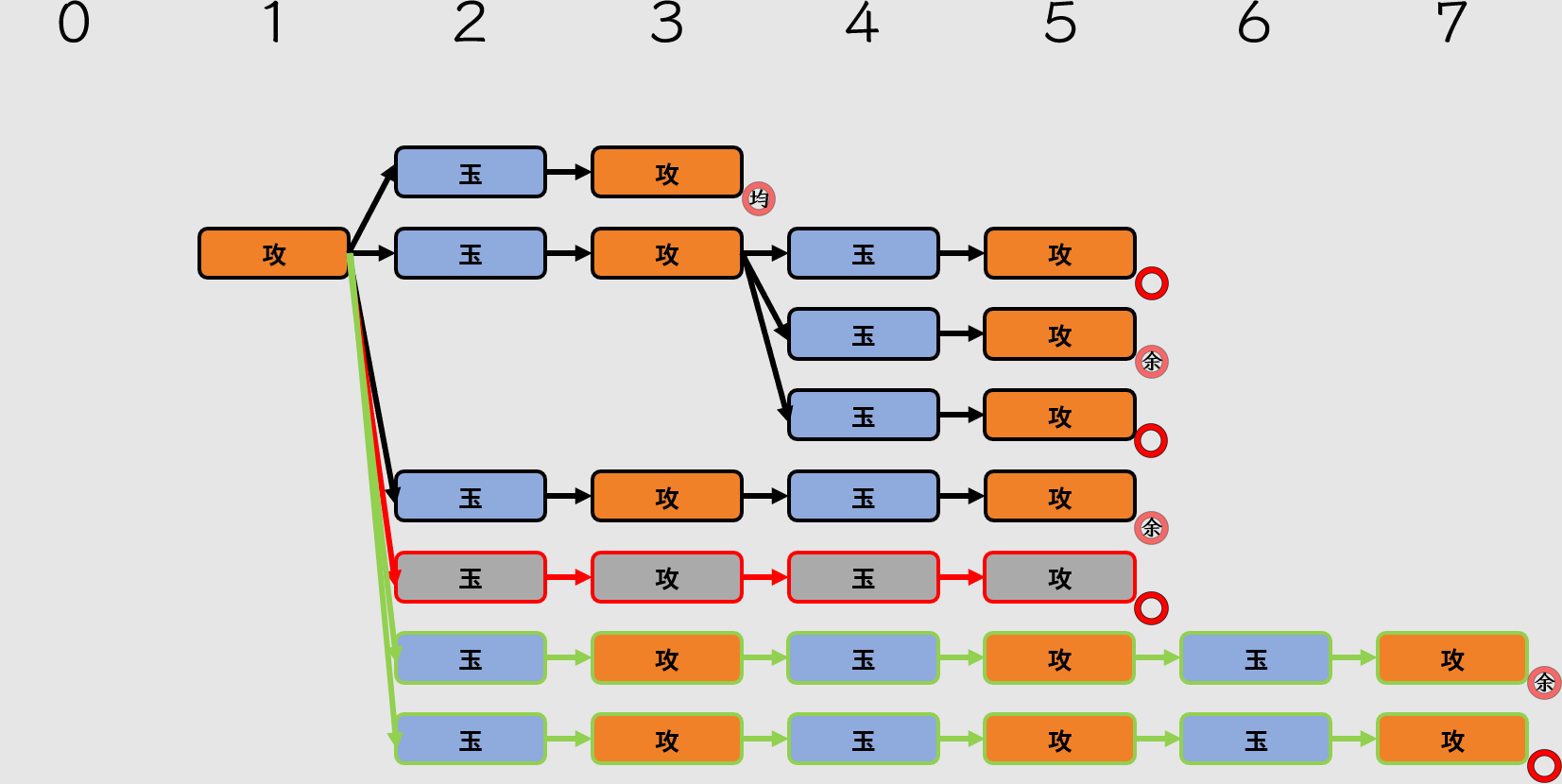新增了綠色分支
應該要保留駒余的長手數分支，還是不駒余的呢？當然是駒余的啦，因為不駒余的變化長手數會直接取代本詰，無法再被視為變化。
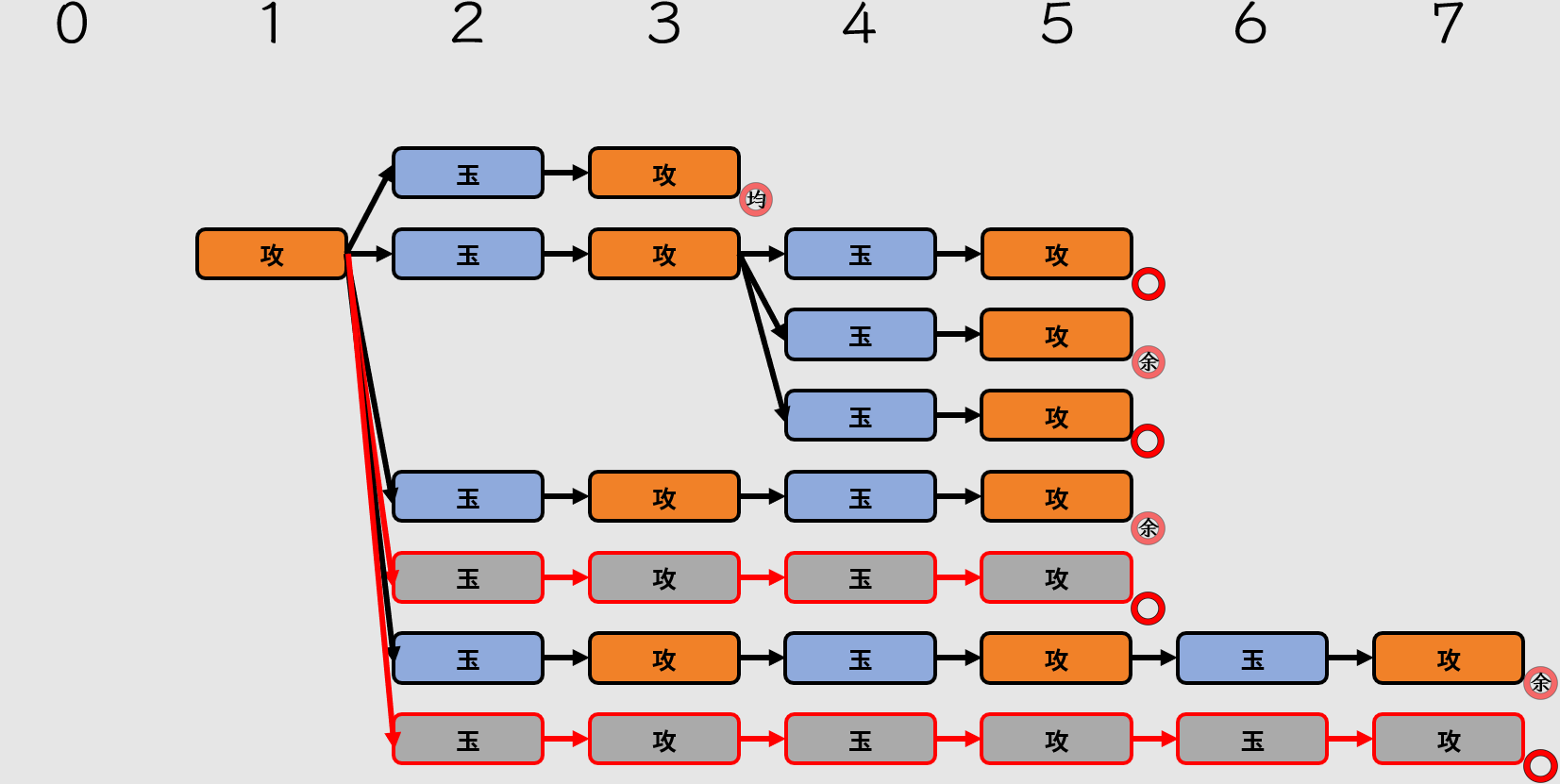二手變長可以算成變化
二手變長並不限於在哪處發生分歧，所以我們把手順圖補完：
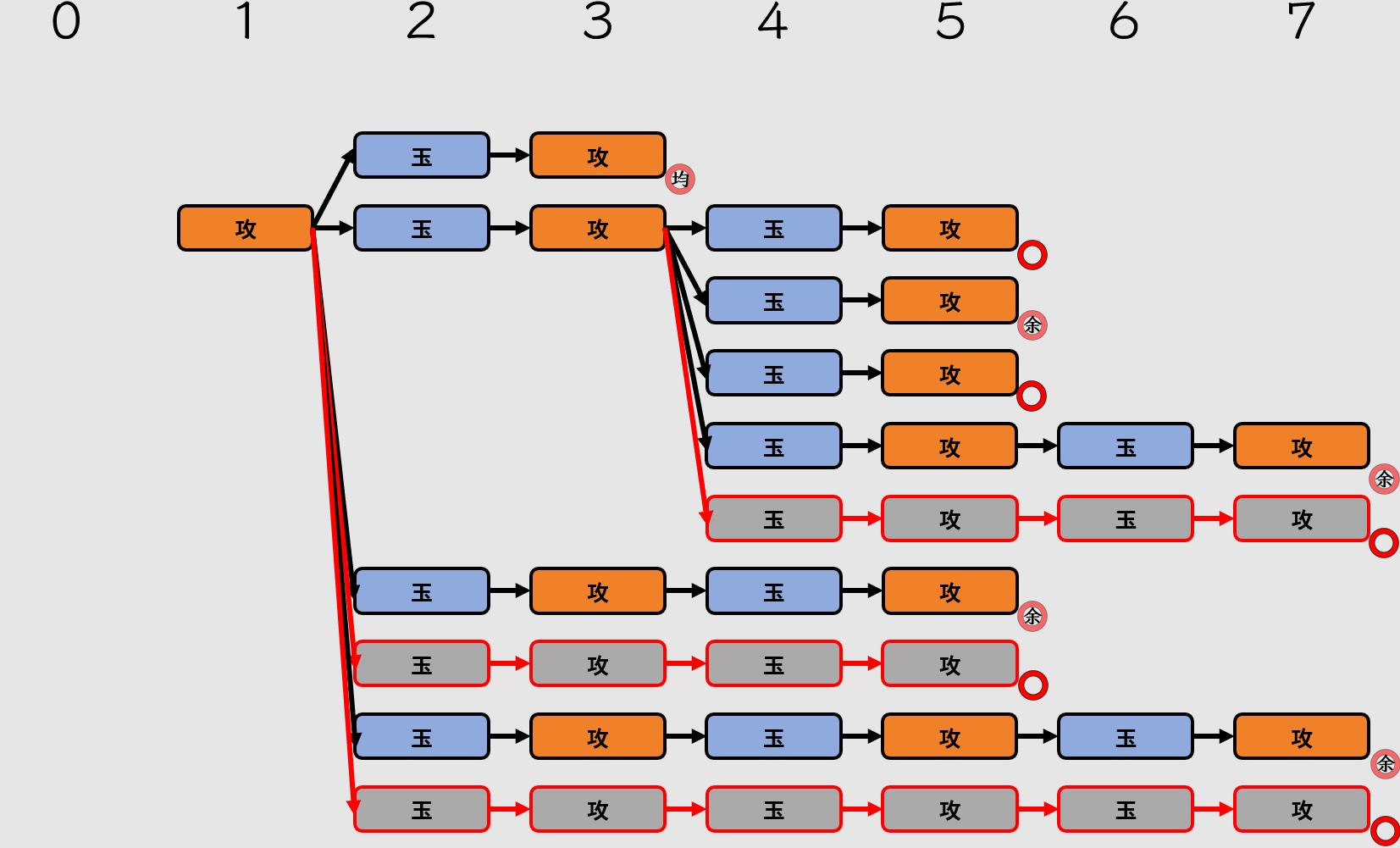驚駭的手順圖
變長
「變長」並不是「變化長手數」的縮寫，實際上是「變化長手數駒余」的縮寫。也因為如此，才會特別強調二手變長可以接受。
變化總結
依照最後的驚駭手順圖，我們再一起回顧一次每條分支，從上到下開始計數。
紛れ
當攻擊方發生分歧時，稱之為「紛れ」。紛れ本身並不含有「詰」的涵義，紛れ可以有詰，也可以沒有詰。
一題完美的詰將棋，必須讓所有的紛れ都不詰，只要有一個紛れ有詰，本題詰將棋將被視為余詰。余詰屬於重大缺陷，會使該題直接變不完全作。無論是否存在駒余，只要紛れ有詰都不被允許。
紛れ因為不能有詰，所以紛れ的變化沒有像變化那樣有很多變化 。
變化的余詰？
紛れ不能有詰
不詰的分支，討論有無駒余意義不大，所以圖片的詰與不詰分支將使用「均」的符號來表示。
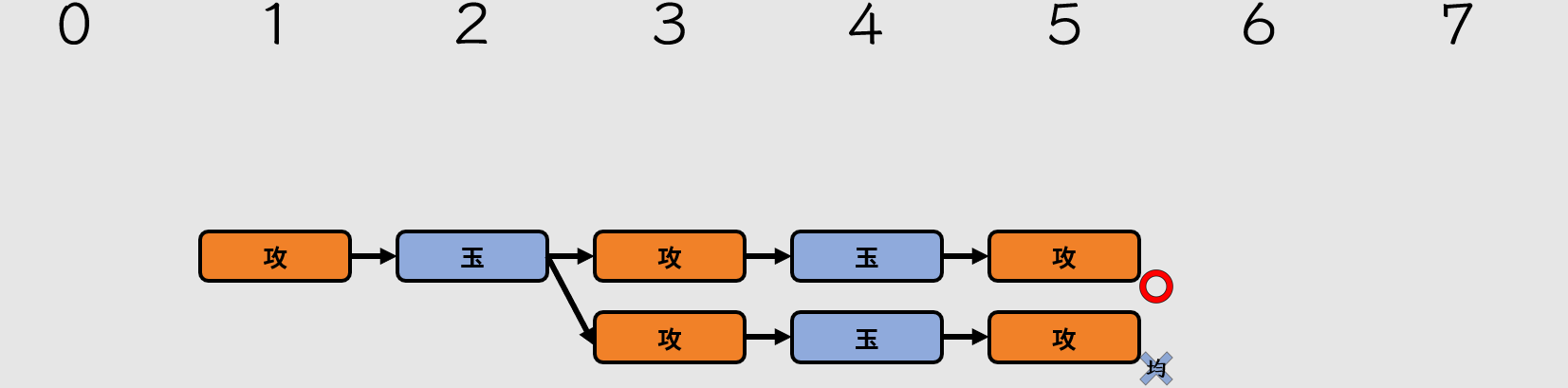紛れ不能有詰
當紛れ出現詰時，即構成余詰，不會出現在可以被採用的「五手詰」中。
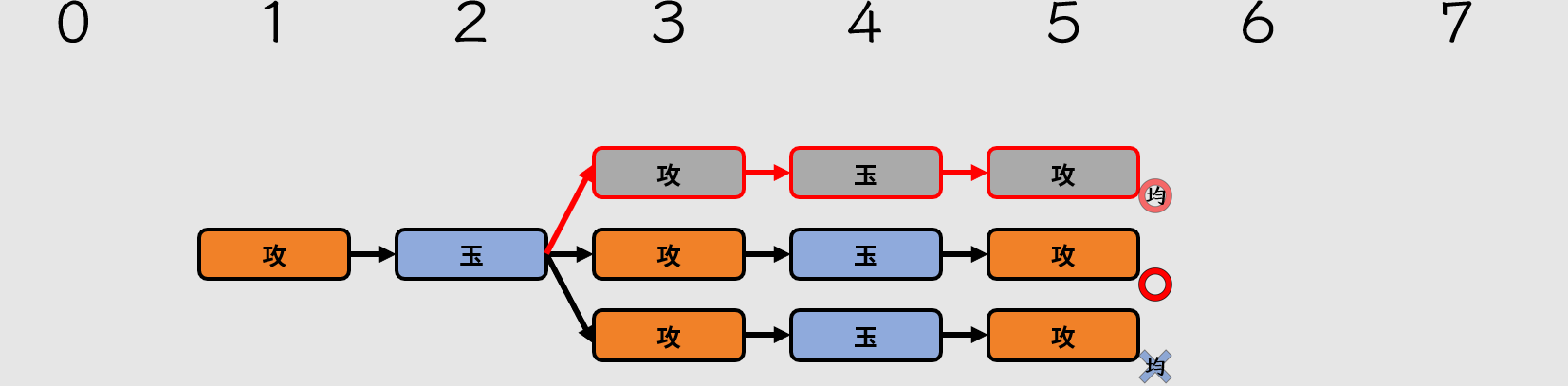不論駒余，紛れ不能有詰
初始玉將方視為唯一
如果在初手出現攻擊方的分歧，應該算作紛れ嗎？
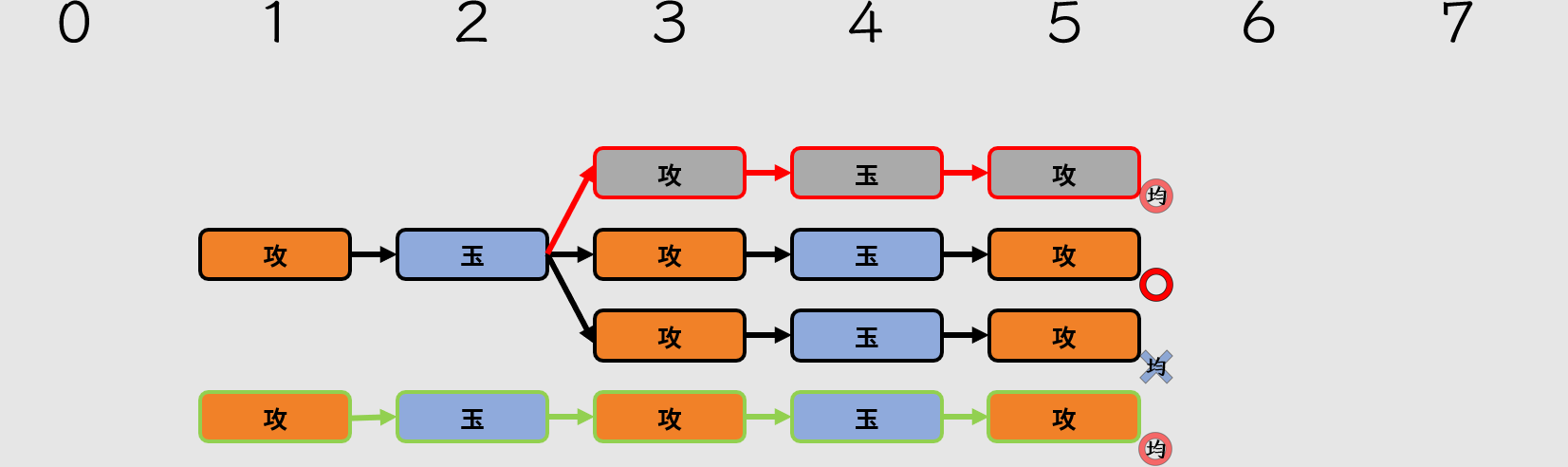新增了綠色分支
這時候，圖片中的第零手終於發揮效用。我們可以將第零手假想成只有一個玉將方的棋步（盤面本身）。因此，剛剛新增的分支也屬於紛れ，同樣也不能有詰。
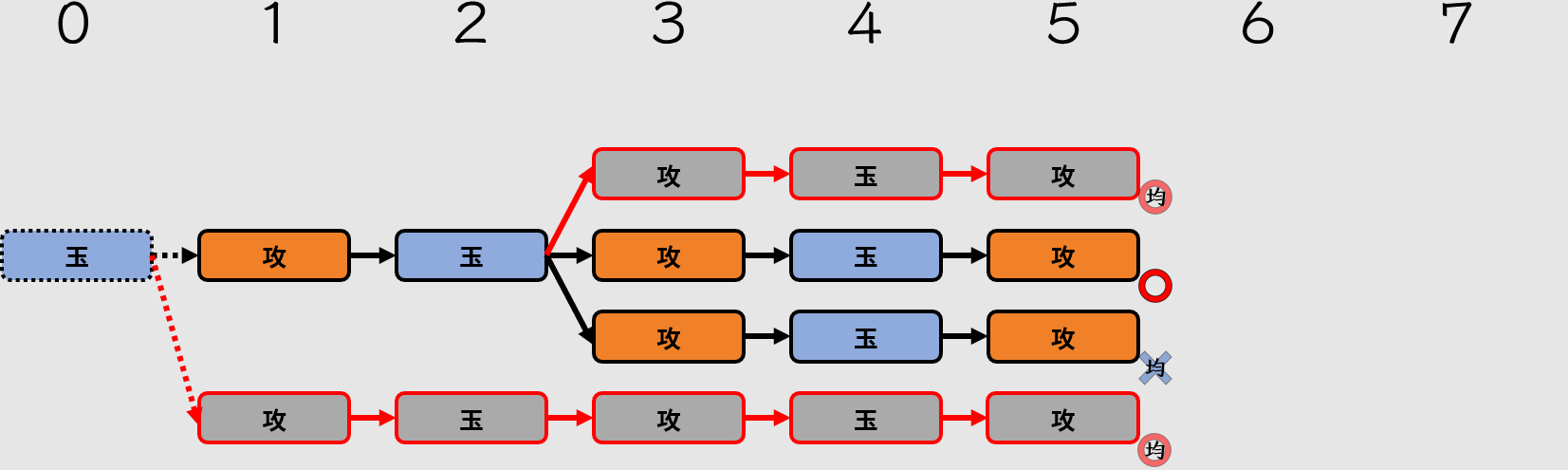虛擬第零手
紛れ短手數
如果紛れ短手數有詰，而「紛れ」等於「攻擊方發生分歧」，這代表攻擊方可以用更短的手數完成詰，那麼本詰就是來搞笑的。
這樣的情況下，紛れ短手數變成本詰；原本的本詰變成紛れ長手數。由於我們假設本詰有詰，所以仍然余詰。
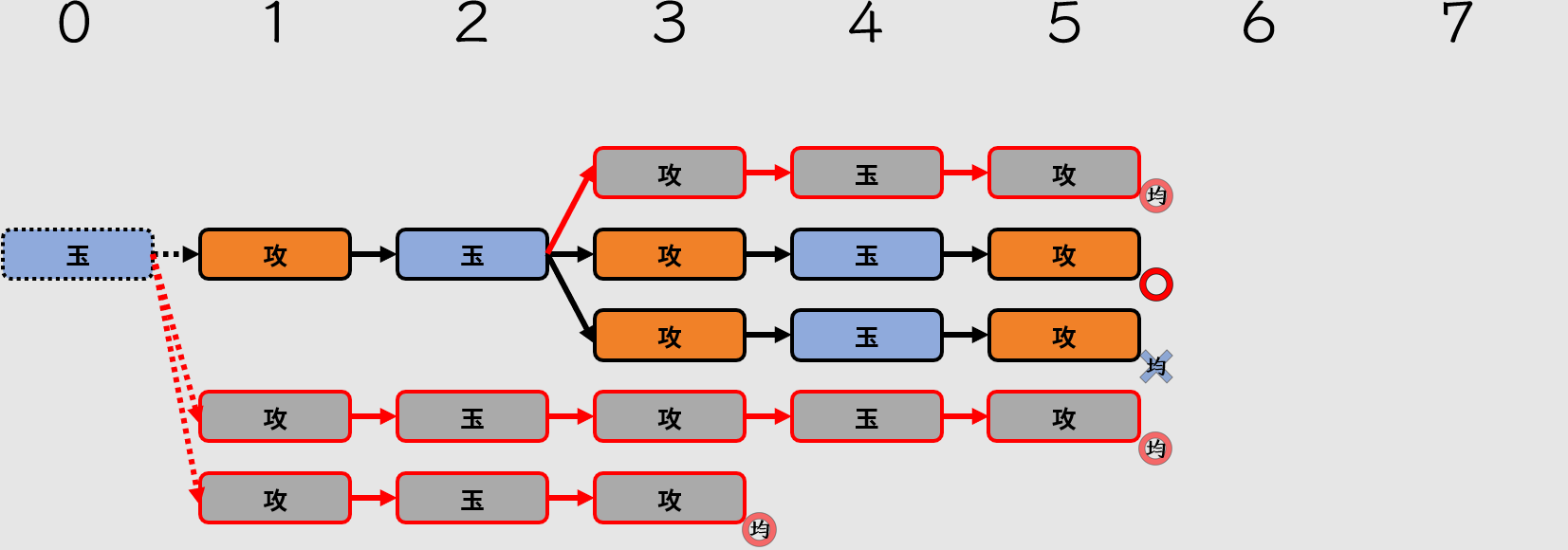紛れ短手數不能有詰
紛れ長手數
雖然紛れ長手數的余詰不會影響本詰的地位（因為攻擊方選擇最短）。但是會對「詰」的唯一性產生威脅。因此，這樣的紛れ長手數余詰依然被視為不能接受的。
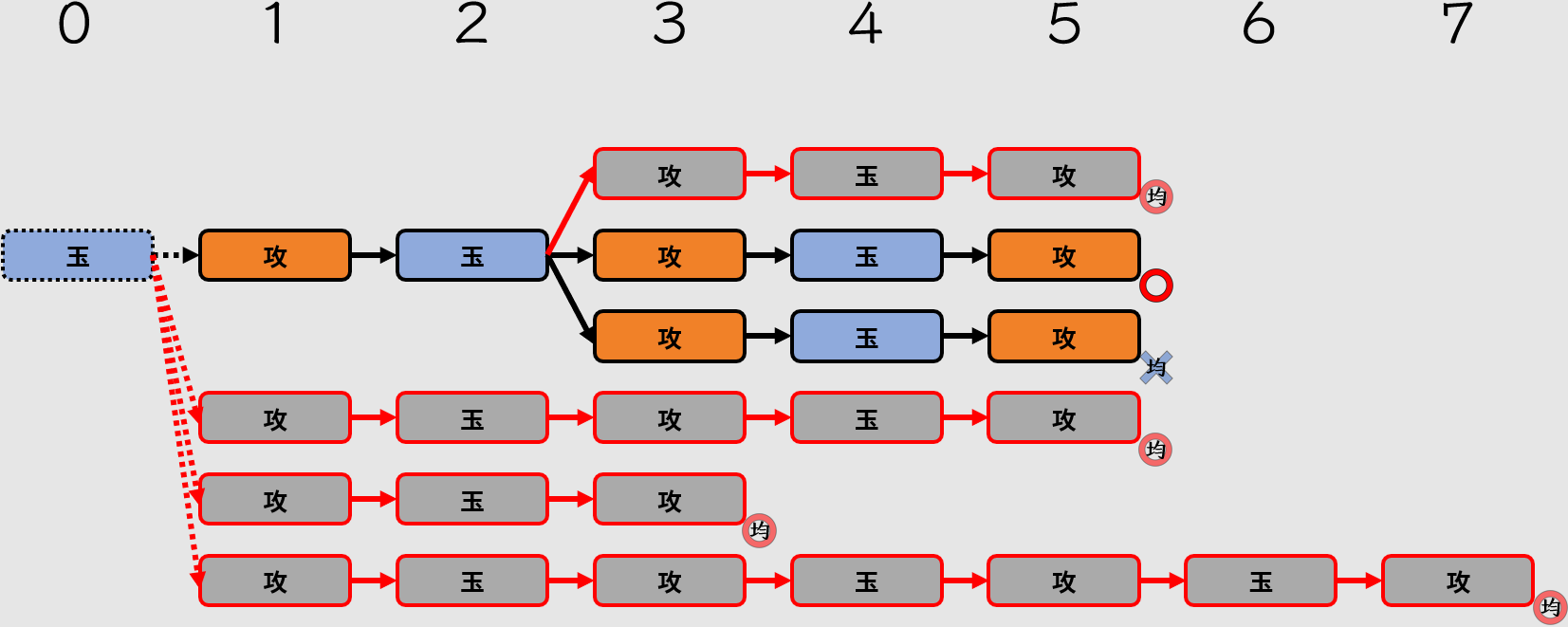紛れ長手數也不能有詰
最終手余詰
當余詰發生在最終手時，是唯一可以被接受的余詰。而且，最終手的余詰是可以駒余的（可以想看看分支圖）。如果最終手余詰駒余，則不會被選為正解手順。
但如果最終手余詰沒有駒余，那就會與本詰有相同地位，正解手順會從本詰與最終手余詰不駒余中，由作者選出認為最精妙的一個。
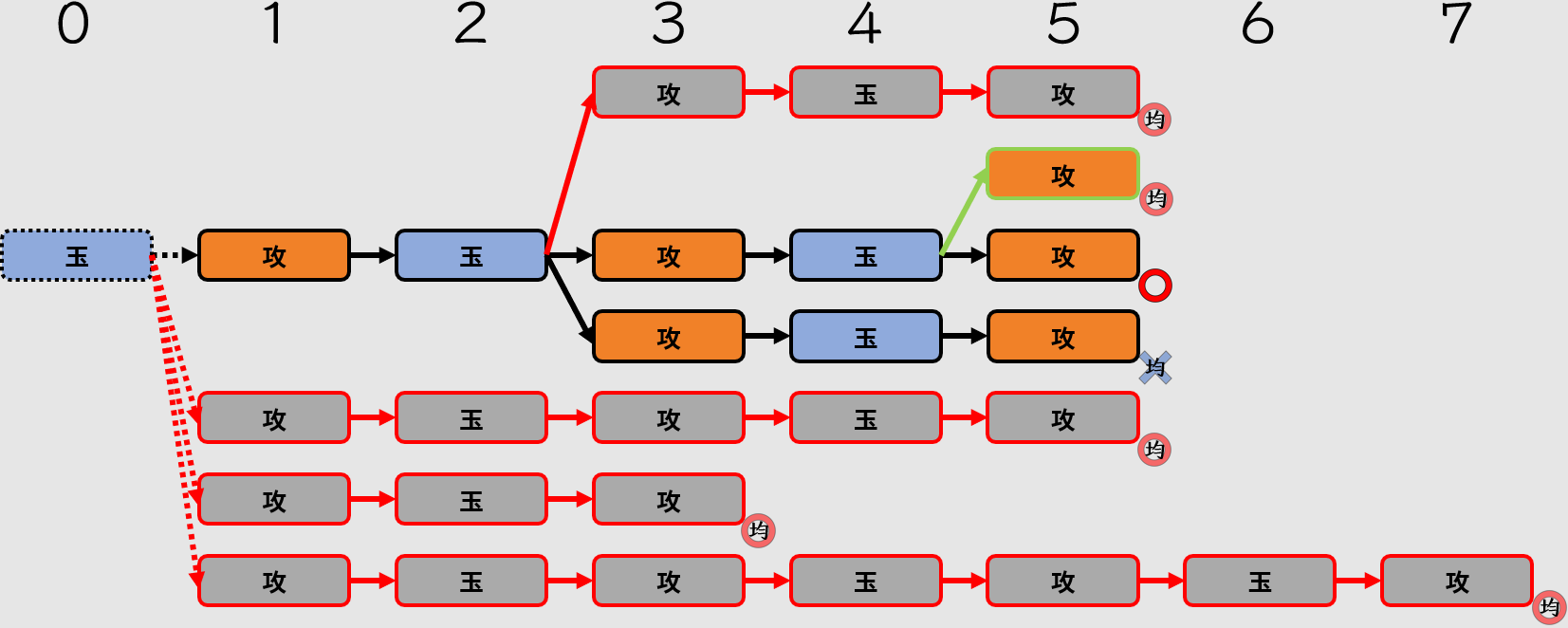最終手余詰的綠色分支可以接受
一手詰的最終手余詰？
攻擊方分歧容許範圍
由於紛れ可能會有余詰的潛在危機，而紛れ的定義還記得是「攻擊方出現分歧」吧。在詰將棋中，某些不同的棋步可以被認定為同一行為，從而避免產生分支。以下這些不同的棋步，我們來討論哪些會被判定為分歧：
-
棋駒不同、位置同
例如：☗５三銀與☗５三金。屬於不同的棋步。
-
棋駒同、位置不同
例如：☗５三銀與☗５四銀。屬於不同的棋步。
-
棋駒同、位置同，成變不同
對於可以成變的棋駒，若在棋步中發揮的效用相同，無論有無成變，可視為同一種棋步。
範例
正解手順為：☗７一角成、☖同玉、☗７二金。其中，初手亦可替換成☗７一角不成，雖然涉及成變不同，但由於效用相同，因此不構成余詰。
發現新大陸作者們在研究詰將棋規則到這裡，已經快要昏頭、焦頭爛額之際，似乎發現了一個漏網之魚。在查閱了大量詰將棋規則後，發現沒有地方提及「玉將方成變不同是否會產生分歧」。
一般來說，討論攻擊方的分歧才是重點，因為怕導致余詰的爭議（例如成變不同與非限定打都是針對攻擊方的判定）。相較之下，玉將方分歧的變化不是越多越好？然而，若考慮到「變同」也是一個缺陷，那麼是否存在這樣的局面——玉將方的應手可以選擇成或不成，且後續手順完全一致？
（出自CrossingVoid）
正解手順為：☗４九桂、☖同銀成、☗６九桂、☖６六玉、☗５七金。其中，第二手亦可替換成☖同銀不成。
若玉將方的成變不同，會被視為不同的棋步，那此題將產生最終四手變同，而不被接受。不過作者本人認為，玉將方應該也能與攻擊方套用相同的規範：若成與不成的效用完全一致，則視為同一種棋步，避免分支。
如果有專門研究詰將棋規則的朋友，歡迎透過棉花糖留言告訴我們您的見解喔！
-
非限定打
對於香車、角行與飛車等遠程攻擊棋駒，若在棋步中發揮的效用相同，無論打入何處，可視為同一種棋步。而如果是金將、銀將等非遠程攻擊棋駒，只要打點不同，就會變成第 2 點的位置不同，會被判定成余詰。不過，非限定打其實算成一個「キズ」。
範例
初手，攻擊方需退路封鎖玉將方，打入角行。但是攻擊方無論☗３四角、☗４三角、☗５二角或☗６一角來退路封鎖玉將方，都可以完成詰，且手數相同。
這類效用相同的遠程攻擊棋駒，即使出現的不同棋步，仍可以被接受。不過部分作者為了臻於完美，會透過「守門員」的方式來化解這類非限定打：
增加９三飛作為守門員。阻擋從☗４三角、☗５二角或☗６一角的角行打入。不過這也只是對作品進行小修小補。
部分設計精良的作品，能夠在不依賴守門員的情況下，僅透過巧妙的佈局，也可讓香角飛只能打在特定位置。這種「限定打」的作品往往能獲得更高的評價。
練習
來練習與欣賞一題限定打題目吧！（提示：初手需要限定打飛車）
Loading...回答正解後，可以思考為何只能打入在那個位置。
附錄：近義名詞比較表
-
變長與變同
與本詰手數比較 是否駒余 備註 變長 大於 
只接受二手變長 變同 等於 
只接受最終二手變同
-
變化與紛れ
由哪方發生分歧 詰將棋要求 違反條件 變化 玉將方 變化都要有詰 變化沒有詰為
不詰紛れ 攻擊方 紛れ都不能有詰 紛れ出現詰為
余詰
變化 -
接受程度比較
不詰 余詰 變同 變長 詰將棋 完全不能接受 最終手余詰可以 最終二手變同可以 二手變長可以 實戰詰將棋 完全不能接受 可以 可以 不可以
（練習 2 會當成問題）
延伸學習：連續打入金將題目探討
在一開始學習詰將棋的詰將棋認識中，大家曾練習過兩題只需連續打入金將即可完成詰殺的題目。
不過，讀到這裡的您，想必已具備判斷詰將棋題目的慧眼。不妨試著跟我們一起延伸這類題目，看看是否違反詰將棋的規則。
頭金題
手順圖
此題無最終手余詰，也無其他缺陷，這題給過！
雙頭金
手順圖
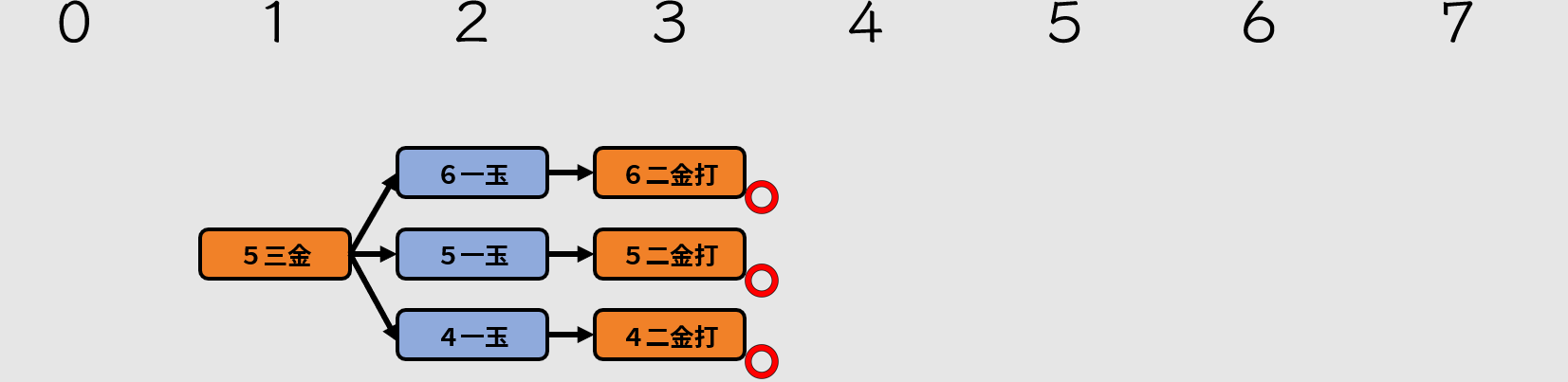
此題玉將方發生分歧，屬於變化範疇。觀察手數皆等長且不駒余，符合變同。看到變同，就要再考慮出現的位置。這題屬於最終二手變同，所以給過！
三頭金
手順圖
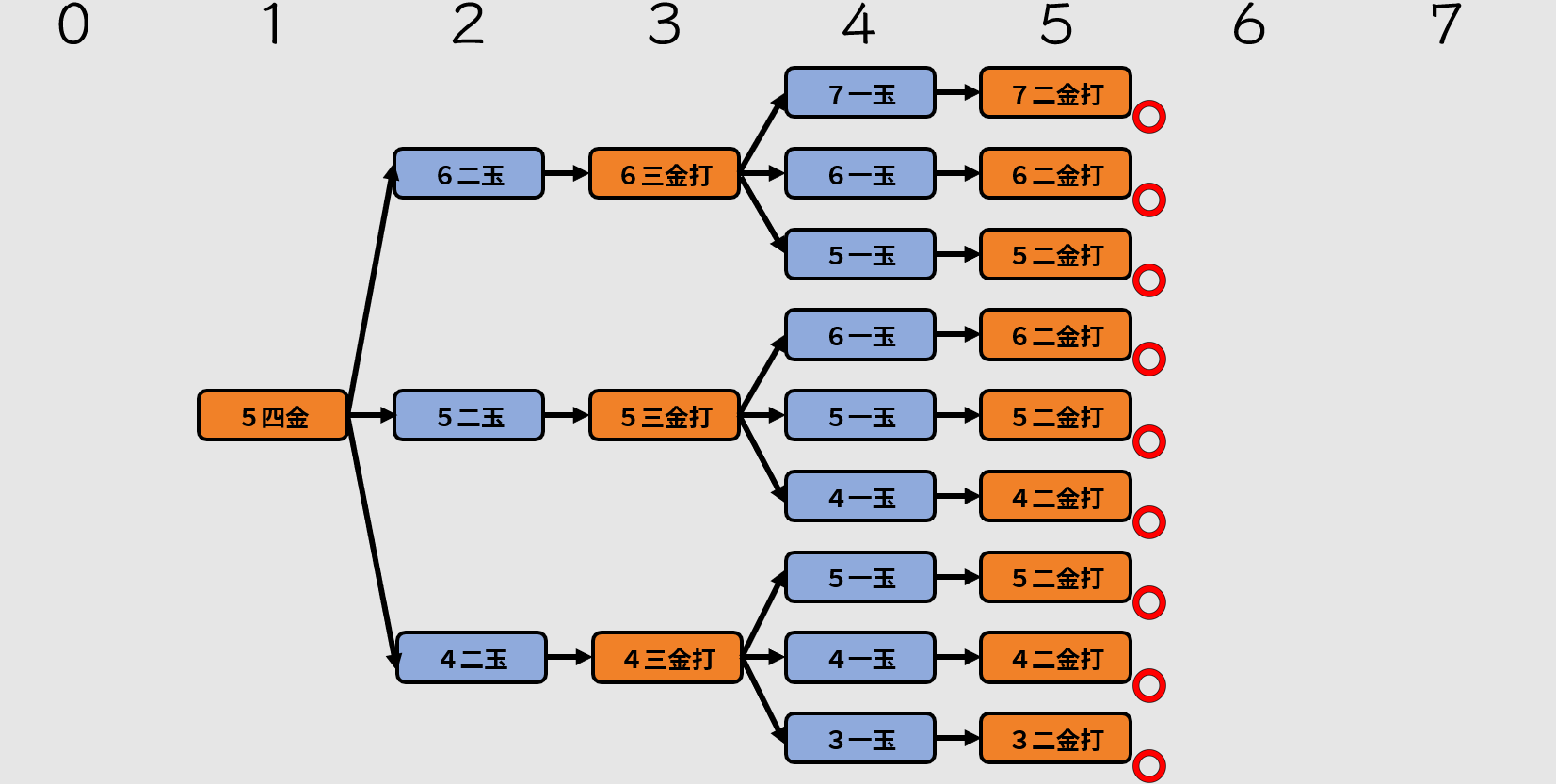
此題玉將方發生分歧，屬於變化範疇。觀察手數皆等長且不駒余，符合變同。看到變同，就要再考慮出現的位置。本題的變同出現在最終四手與最終二手。最終二手變同沒問題，但最終四手變同屬於缺陷，那麼這題打咩……嗎？
其實，詰將棋中有一條我們沒有特別介紹的額外規則：「對稱題目不論從哪一側進攻，皆不算作分歧」。因此，從規則上來說，本題在規則上是站得住腳的。
不過，除了規則之外，還有潛規則啊！詰將棋潛規則：「不要創作無意義的題目」。
以上三題都屬於無意義的題目，因為只需了解金將、玉將與步兵的移動方式，就可以輕而易舉的解開。這類純粹無腦塞金將的題目，就不會被收錄。可以當作練習題，但別說這是詰將棋。沒錯，就是說你，海鮮素！